|
EN BREF
|
Le théorème de Pythagore est un outil fondamental en mathématiques, surtout lorsqu’il s’agit de travailler avec des triangles rectangles. Il établit une relation précise entre les longueurs des côtés de ces triangles. En comprenant ce théorème, vous pourrez facilement calculer la longueur d’un côté inconnu, à condition de connaître les longueurs des deux autres côtés. Dans les lignes suivantes, nous allons explorer ce calcul de manière simple et accessible, afin de dissiper les éventuelles complexités liées à son utilisation.
Le théorème de Pythagore est l’un des concepts fondamentaux en mathématiques qui s’applique aux triangles rectangles. En quelques étapes simples, vous pouvez apprendre à calculer la longueur d’un côté d’un triangle rectangle en utilisant les longueurs des deux autres côtés. Que vous soyez un élève cherchant à améliorer vos compétences ou simplement curieux de ce principe mathématique, cet article vous guidera à travers les étapes clés pour appliquer ce théorème de manière efficace.
Comprendre le théorème de Pythagore
Le théorème de Pythagore stipule qu’« dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés ». En d’autres termes, si l’on désigne les côtés adjacents à l’angle droit comme A et B, et l’hypoténuse comme C, on peut écrire la formule suivante : C² = A² + B².
Utiliser le théorème de Pythagore pour des calculs
Pour appliquer ce théorème dans des problèmes pratiques, il suffit de suivre quelques étapes simples. Vous devez d’abord identifier les longueurs des deux côtés adjacents au coin droit. Supposons par exemple que vous ayez un triangle rectangle avec les côtés mesurant 3 unités et 4 unités. En appliquant la formule du théorème de Pythagore, vous allez faire le calcul suivant :
C² = 3² + 4²
Ce qui donne :
C² = 9 + 16 = 25
Ensuite, pour trouver C, vous devez prendre la racine carrée de 25, ce qui donne :
C = 5
Ainsi, l’hypoténuse mesure 5 unités.
Exemples pratiques pour illustrer
Voyons un autre exemple. Imaginons un triangle rectangle pour lequel les longueurs des cathètes sont respectivement de 5 et 12 unités. Pour trouver l’hypoténuse, on utilise à nouveau la formule :
C² = 5² + 12²
Ce qui revient à :
C² = 25 + 144 = 169
Dès lors, pour obtenir C, vous récupérez :
C = √169 = 13
Donc, dans ce cas, l’hypoténuse mesure 13 unités.
Vérification si un triangle est rectangle
Le théorème de Pythagore n’est pas seulement utile pour calculer la longueur d’un côté, mais également pour déterminer si un triangle donné est effectivement rectangle. Pour cela, vous comparez le carré de la longueur du côté le plus long à la somme des carrés des longueurs des deux autres côtés. Si l’égalité est vérifiée, c’est qu’il s’agit bien d’un triangle rectangle.
Par exemple, si vous avez un triangle avec des côtés de longueurs 8, 15 et 17, vous appliquez le théorème :
17² ? (8² + 15²)
Ce qui vous donne :
289 ? (64 + 225) = 289
Puisque l’égalité est respectée, le triangle est bien rectangle.
En maîtrisant le théorème de Pythagore, vous pouvez facilement effectuer des calculs concernant les triangles rectangles. Il suffit d’appliquer la formule de manière systématique et de bien connaître les longueurs des côtés. Ce théorème est non seulement fondamental pour les études en mathématiques, mais il est également extrêmement utile dans de nombreux domaines tels que l’architecture, l’ingénierie, et même dans les situations de la vie quotidienne.
Calcul simple du théorème de Pythagore
| Étapes | Explication concise |
| Identifier les côtés | Distinguer les deux cathètes et l’hypoténuse. |
| Mesurer les cathètes | Consigner les longueurs des deux cathètes, notées a et b. |
| Appliquer la formule | Utiliser la formule : c² = a² + b², où c est l’hypoténuse. |
| Calculer les carrés | Calculer a² et b² séparément. |
| Sommer les carrés | Ajouter les résultats : a² + b². |
| Radical pour c | Calculer la racine carrée du total pour obtenir c : c = √(a² + b²). |
| Vérification | Vérifier que la relation est valide pour un triangle rectangle. |
Le théorème de Pythagore est un outil puissant en géométrie, essentiel pour déterminer les longueurs des côtés d’un triangle rectangle. Il repose sur une relation simple entre les longueurs des côtés de ce triangle. Dans cet article, nous dévoilons une méthode simple pour effectuer ce calcul et l’appliquer facilement dans divers problèmes.
Comprendre les éléments du théorème
Le théorème de Pythagore s’énonce de manière concise : dans un triangle rectangle, le carré de la longueur de l’hypoténuse (le côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés, appelés cathètes. Cette relation s’écrit mathématiquement comme suit : c² = a² + b², où c est l’hypoténuse, et a et b sont les cathètes.
Étape par étape : Comment effectuer le calcul
Pour appliquer le théorème de Pythagore, suivez ces étapes simples :
1. Identifiez les côtés du triangle : Déterminez quelles sont les longueurs des cathètes et de l’hypoténuse. Par exemple, pour un triangle avec des côtés mesurant 3 et 4 unités, labellez-les respectivement comme a et b.
2. Appliquez la formule : Utilisez la formule c² = a² + b². Dans notre exemple, calculez : c² = 3² + 4².
3. Calculez les carrés : Effectuez les opérations pour obtenir c² = 9 + 16.
4. Additionnez les résultats : Cela donne c² = 25.
5. Trouvez la racine carrée : Pour obtenir la longueur de l’hypoténuse, prenez la racine carrée de 25, ce qui donne c = 5.
Exemple pratique
Imaginons un triangle rectangle DEF, où l’angle droit est au point E. Supposons que les longueurs des cathètes DE et EF mesurent respectivement 5 cm et 12 cm. Utilisons le théorème de Pythagore pour découvrir la longueur de DF :
1. Identifiez les cathètes : ici, DE = 5 cm et EF = 12 cm.
2. Appliquez la formule : DF² = DE² + EF², soit DF² = 5² + 12².
3. Calculez : DF² = 25 + 144, donc DF² = 169.
4. Trouvez la racine carrée : DF = √169, ce qui donne DF = 13 cm.
Utilisation du théorème dans la vie quotidienne
Le théorème de Pythagore n’est pas seulement une théorie abstraite ; il trouve des applications dans de nombreux domaines de la vie quotidienne. Que ce soit pour construire des maisons, pour des projets artistiques ou pour des calculs en navigation, comprendre et utiliser le théorème de Pythagore est indispensable. Avec cet outil, chacun peut résoudre rapidement des problèmes géométriques simples, rendant ainsi les mathématiques plus accessibles.
- Identifier le triangle rectangle: Assurez-vous que le triangle est bien rectangle.
- Dénommer les côtés: Nommez les côtés comme suit : AC et BA pour les cathètes, et BC pour l’hypoténuse.
- Appliquer la formule: Utilisez la formule BC² = AC² + BA².
- Calculer les carrés: Calculez les carrés des longueurs des cathètes.
- Ajouter les résultats: Additionnez les résultats des carrés des cathètes.
- Prendre la racine carrée: Extrayez la racine carrée de la somme obtenue pour trouver l’hypoténuse ou l’un des côtés.
- Vérifier le triangle: Si vous avez les longueurs et que cela respecte la formule, c’est un triangle rectangle.
Comprendre le théorème de Pythagore
Le théorème de Pythagore est un principe fondamental de la géométrie qui s’applique aux triangles rectangles. En termes simples, il stipule que, dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Cet article vous guide pas à pas pour apprendre à le calculer en toute simplicité.
Identification des côtés d’un triangle rectangle
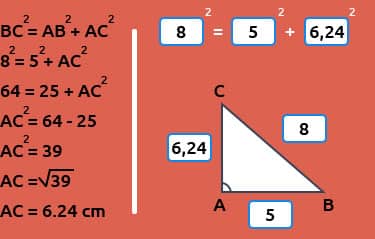
Avant d’appliquer le théorème, il est crucial d’identifier les différents côtés du triangle rectangle. On désigne généralement les côtés adjacents à l’angle droit par AC et BA, appelés cathètes, et le côté opposé à l’angle droit par BC, qui est l’hypoténuse.
Notions de base du théorème
La formule du théorème de Pythagore peut être écrite comme suit :
BC² = AC² + BA²
Cette relation signifie que si vous connaissez les longueurs des deux cathètes, vous pouvez facilement trouver la longueur de l’hypoténuse simplement en additionnant les carrés de ces longueurs.
Calculer la longueur d’un côté
Supposons que vous ayez un triangle rectangle avec les longueurs des cathètes AC = 3 cm et BA = 4 cm. Pour trouver la longueur de l’hypoténuse, vous n’avez qu’à appliquer la formule mentionnée :
BC² = AC² + BA²
En remplaçant les valeurs, on obtient :
BC² = 3² + 4²
BC² = 9 + 16
BC² = 25
Ensuite, pour obtenir BC, il suffit de prendre la racine carrée de 25 :
BC = √25 = 5 cm
Utiliser le théorème pour vérifier un triangle rectangle
Le théorème de Pythagore peut aussi être utilisé pour vérifier si un triangle donné est effectivement un triangle rectangle. Supposons que vous ayez un triangle avec les côtés mesurant a = 5 cm, b = 12 cm et c = 13 cm. Pour déterminer si ce triangle est rectangle, appliquez la formule :
c² = a² + b²
En remplaçant les longueurs, cela donne :
13² = 5² + 12²
169 = 25 + 144
169 = 169
Comme l’égalité est vérifiée, le triangle avec ces dimensions est bien un triangle rectangle.
Pratique avec des exemples
Pour maîtriser le théorème de Pythagore, il est essentiel de s’exercer avec différents exemples. Par exemple, dans un triangle rectangle où l’un des côtés mesure 8 cm et les deux autre cathètes sont 6 cm, vous pouvez pratiquer le calcul de l’hypoténuse ou vérifier si un triangle est rectangle. Créez plusieurs scénarios et essayez de résoudre les problèmes sans aide.
En suivant ces étapes simples et en vous entraînant avec différents triangles, vous serez capable de maîtriser le théorème de Pythagore et de l’appliquer avec confiance dans vos calculs de géométrie. N’oubliez pas que la pratique est essentielle pour devenir habile dans son utilisation.